

Usually, these definitions are equivalent in the special, but important case Several slightly different definitions can be found in the
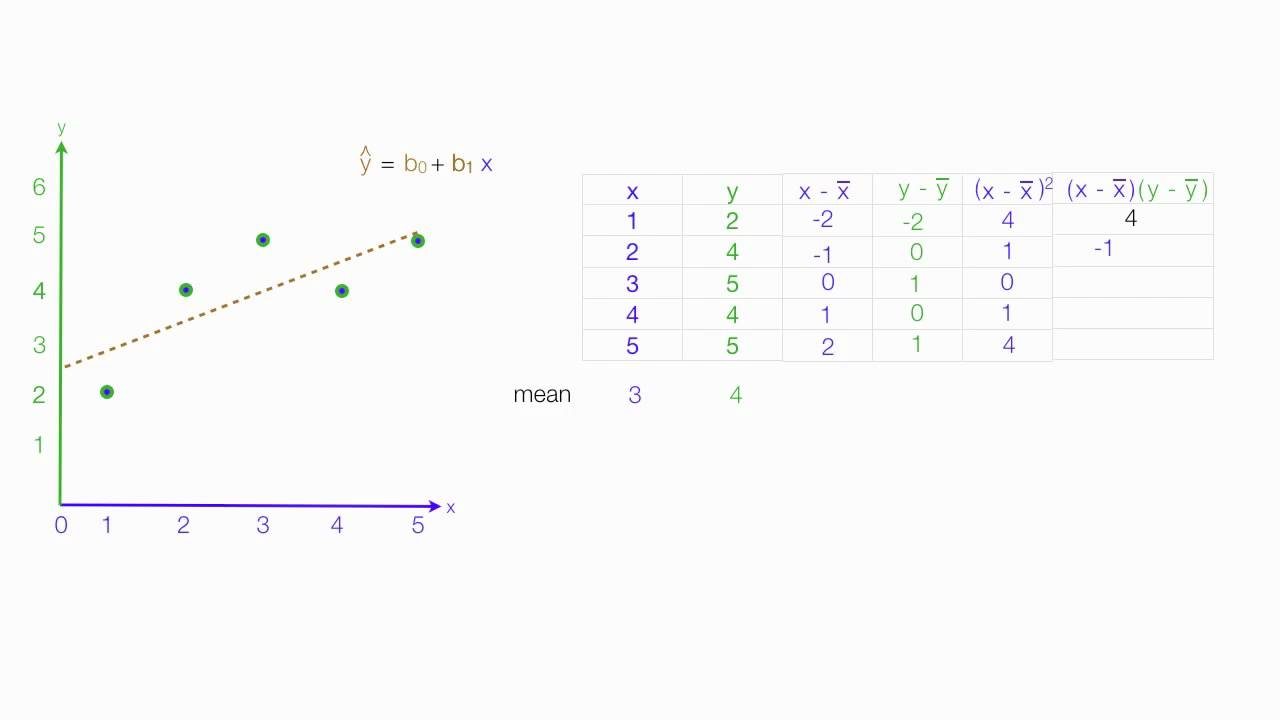
The intercept of the fitted line is such that the line passes through the center of mass ( x, y) of the data points.More details about the degrees-of-freedom adjustmentīefore defining the R squared of a linear regression, we warn our readers that In this case, the slope of the fitted line is equal to the correlation between y and x corrected by the ratio of standard deviations of these variables. The remainder of the article assumes an ordinary least squares regression. Deming regression (total least squares) also finds a line that fits a set of two-dimensional sample points, but (unlike ordinary least squares, least absolute deviations, and median slope regression) it is not really an instance of simple linear regression, because it does not separate the coordinates into one dependent and one independent variable and could potentially return a vertical line as its fit. Other regression methods that can be used in place of ordinary least squares include least absolute deviations (minimizing the sum of absolute values of residuals) and the Theil–Sen estimator (which chooses a line whose slope is the median of the slopes determined by pairs of sample points). It is common to make the additional stipulation that the ordinary least squares (OLS) method should be used: the accuracy of each predicted value is measured by its squared residual (vertical distance between the point of the data set and the fitted line), and the goal is to make the sum of these squared deviations as small as possible. The adjective simple refers to the fact that the outcome variable is related to a single predictor. That is, it concerns two-dimensional sample points with one independent variable and one dependent variable (conventionally, the x and y coordinates in a Cartesian coordinate system) and finds a linear function (a non-vertical straight line) that, as accurately as possible, predicts the dependent variable values as a function of the independent variable. In statistics, simple linear regression is a linear regression model with a single explanatory variable. Here the dependent variable (GDP growth) is presumed to be in a linear relationship with the changes in the unemployment rate. Okun's law in macroeconomics is an example of the simple linear regression. Linear regression model with a single explanatory variable Part of a series on


 0 kommentar(er)
0 kommentar(er)
